The Quicksort Algorithm or Partition-Exchange Sort is a method of sorting that uses the divide and conquer design pattern which breaks down a problem into smaller pieces recursively until the problem because simple enough to solve directly. The actual algorithm was first developed back in 1959 by the British computer scientist Tony Hoare and is widely used today as a efficient means of sorting. As a software developer its hugely beneficial to know and understand the algorithm and its implementation. JavaScript has a built in sort function that uses Insertion Sort by Chrome’s V8 Engine and Merge Sort by Safari and Mozilla Firefox, so you might be asking why even bother learning about Quicksort? Well other than just adding another tool to your coding tool chest that you can tweak to work for specific scenarios when you need to, you can use the sort functionality for allot of times when you need to sort elements and is fine until you are dealing with very large datasets with many many elements, in these cases Quicksort is a more efficient algorithm to use.

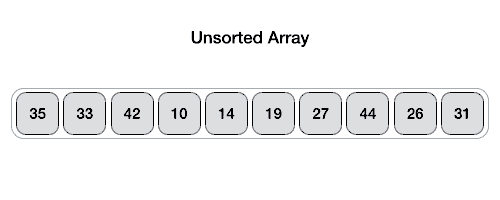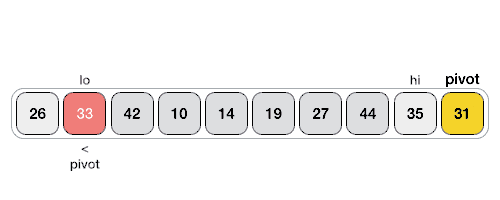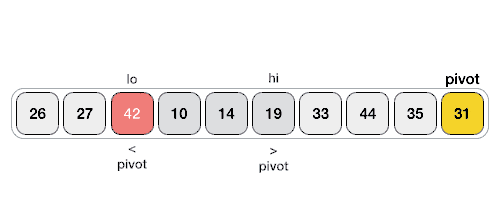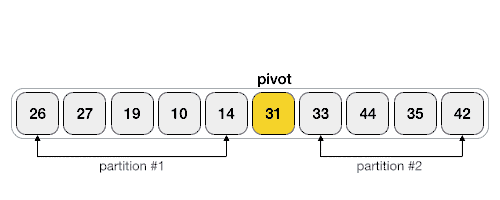
Basic flow pseudocode of the algorithm.

1. Make the right-most index value pivot
2. partition the array using pivot value
3. quicksort left partition recursively
4. quicksort right partition recursively

So for the first part of the algorithm we need to have the main function which we will call quickSort.

function quickSort(items, left = 0, right = items.length-1){
  let index;

  if (items.length > 1){
    index = partition(items, left, right);
    if (left < index - 1){
      quickSort(items, left, index - 1);
    }
    if (index < right){
      quickSort(items, index, right);
    }
  }
  return items;
}

Here we have the first argument items which is the array passed into the function and two other arguments left and right representing the low and high index positions of the array. We set default values for the left argument to be 0 (the starting index position) and items.length-1 for the right variable (for the end index position). This way we can just pass in a array if we want to but we need to have the left and right arguments so that when we call the quickSort function on the smaller parts of the array we can specify the start and end for that partition.

We then check to make sure that the length of the array is greater than 1, and if not then just return the array. Now we set the main index position by calling a function called partition which will pick the pivot and do some sorting then return the left index position. The next two if then statements are checking whether there are more elements on the to the left of the main index or the right of the main index position, and call quickSort on them.

Now we have to write our partition function.

function partition(items, left, right){
  let pivot = items[Math.floor((right+left)/2)]
  let l = left;
  let r = right;

  while (l <= r){
    if (items[l] < pivot){
      l++;
    }
    if (items[r] > pivot){
      r--;
    }
    if (l <= r){
      swap(items, l, r);
      l++;
      r--;
    }
  }
  return l;
}

As you can see the we pass in the elements and left and right position as arguments again, then we pick a pivot by dividing the length of the left and right index positions to get a element roughly in the middle of that range as well as setting a l and r variable that represents the left and right index positions for this function while we iterate through the array from both sides. The while loop runs as long as the l variable is less than or equal to the r variable. The next two if then statements will increment the l and decrement the r index values until we have a element at index position l that is greater than the pivot element and a element at the index position r that is less than the pivot element. When each of those conditions are met we simply swap those two elements and again increment the l index and decrement the r index.

For the swapping of elements lets write a simple swap function to take of it.

function swap(items, left, right){
  let temp = items[left];
  items[left] = items[right];
  items[right] = temp;
}

Again as with the previous two functions we are taking a items and a left and right index as arguments, we then set a temp variable as a place holder for the value in the left index position, set the value of items[left] to be the value at items[right] then set the value of items at index right to equal the value of the temp variable. Note that throughout this process we are passing the actual array into each function so we are working on the same array and as a result we don’t need to return it each time.

And that’s how you implement the Quicksort algorithm in JavaScript, its really not very complex but hugely useful and personally gave me a good understanding on how to implement recursion in code why you would want to. If you’re still struggling with understanding exactly whats going on during the actual execution of the code and are a visual learner like me you can take a look at the how the state of all the variables at each step in the process by running this code in a JavaScript Visualizer.

Here is the code all together.

function swap(items, left, right){
  let temp = items[left];
  items[left] = items[right];
  items[right] = temp;
}

function partition(items, left, right){
  let pivot = items[Math.floor((right+left)/2)]
  let l = left;
  let r = right;

  while (l <= r){
    if (items[l] < pivot){
      l++;
    }
    if (items[r] > pivot){
      r--;
    }
    if (l <= r){
      swap(items, l, r);
      l++;
      r--;
    }
  }
  return l;
}



function quickSort(items, left = 0, right = items.length-1){
  let index;

  if (items.length > 1){
    index = partition(items, left, right);
    if (left < index - 1){
      quickSort(items, left, index - 1);
    }
    if (index < right){
      quickSort(items, index, right);
    }
  }
  return items;
}